Data Analysis 2.4

Search the site...

Sentry Page Protection

Data Analysis [14-15]

N-way Crosstabulation Table

So far, we have learned how to create a 1-way frequency table that focuses on a single categorical variable.

The n-way crosstabulation table offers insights about the relationship between multiple categorical variables.

Example

Data CS;
Input Record $ Gender $ Rating $;
Datalines;
RD001 Male A
RD002 Male B
RD003 Female C
RD004 Male A
RD005 Male B
RD006 Male B
RD007 Female D
RD008 Male D
RD009 Female C
RD010 Female C
RD011 Female D
RD012 Male A
RD013 Female A
RD014 Male A
RD015 Female C
RD016 Male A
RD017 Female D
RD018 Male B
RD019 Female C
RD020 Female A
;
Run;

The CS data set contains a list of customer service rating along with the customers' gender.

There are 4 rating options (A, B, C and D).

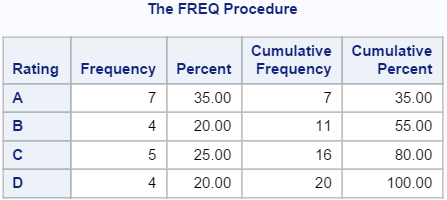
Let's take a look at the frequency distribution of the customer service rating alone.

Example

Proc Freq Data=CS;
Table Rating;
Run;

The rating looks decent. More than 50% of the rating is either A or B.

Now, let's take a look at the result of a 2-way crosstabulation table with Gender and Rating.

Example

Proc Freq Data=CS;
Table Gender*Rating;
Run;

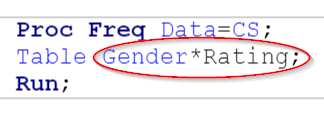
To create the 2-way crosstabulation table, you must add the two variables to the TABLE statement separated by an asterisk.

In our example, the TABLE statement is:

Table Gender * Rating;

This tells SAS to create the crosstabulation table across Gender and Rating:

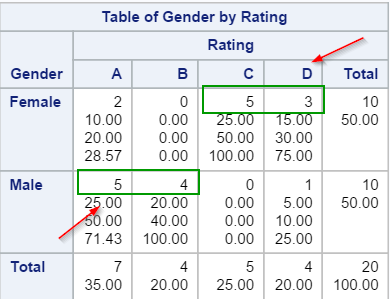
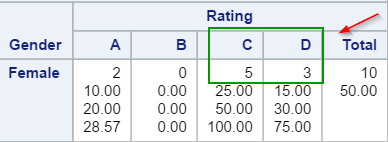
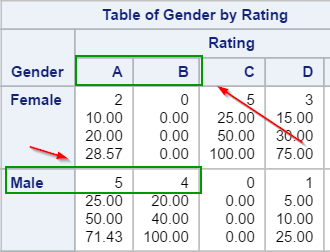
The 2-way table shows the rating statistics across both genders.

The female customers responded with mostly negative rating, with 5 rated the service a C's and 3 rated a D's.

This is clearly in contrast with the male's rating, where 5 rated a A's and 4 rated a B's.

By looking at the 2-way crosstabulation table, the company might want to invest resources in providing better services to their female customers.

Exercise

Copy and run the TRTMT data set from the yellow box below:

Data Trtmt;
Infile Datalines dsd;
Input PSID $ Trt :$20. Days;
Datalines;
ID251,Real Treatment,2
ID252,Placebo,1
ID253,Real Treatment,3
ID254,Real Treatment,2
ID255,Placebo,2
ID256,Placebo,4
ID257,Placebo,2
ID258,Placebo,5
ID259,Real Treatment,4
ID260,Real Treatment,2
ID261,Real Treatment,3
ID262,Placebo,2
ID263,Real Treatment,1
ID264,Real Treatment,2
ID265,Placebo,3
ID266,Real Treatment,1
ID267,Placebo,0
ID268,Placebo,2
ID269,Real Treatment,0
ID270,Placebo,2
;
Run;

The TRTMT data set contains the treatment information from a depression study.

Below are the 3 variables in the data set:

PSID: Patient ID
Trt: Treatment (Real or Placebo)
Days: The number of days where the patient had a sleepless night (symptom of stress and depression)

Create a 2-way crosstabulation table across Trt and Days. Briefly describe whether the treatment is more effective than the placebo.

Need some help?

HINT:
The two variables of interest should be placed in the TABLE statement separated by an asterisk ( * ).

SOLUTION:
Proc Freq Data=Trtmt;
Table Trt*Days;
Run;

The patients taking the real treatment does not seem to have better sleep over those taking the placebo.

40% of the treatment group and 50% of the placebo group reported having 2 sleepless nights a week. 90% of the treatment group and 80% of the placebo group have no more than 3 sleepless nights.

The results are quite similar between the two groups.

Is the difference between the two groups statistically significant? This can be answered by the Fisher-exact test, which will be explained in the next module.

Fill out my online form.