Sentry Page Protection
Statistical Analysis [2-7]
One-sided t-test
A one-sided t-test can be used to test whether the sample mean is significantly larger or smaller than a hypothesized value.
Example
Copy and run the WATER data set from the yellow box below.
Example
Copy and run the WATER data set from the yellow box below.
The WATER data set contains a list of 100 tap water samples with the corresponding chloride level.
The recommended chloride concentration for tap water is not to exceed 250 mg/L.
The Ministry of Environment in British Columbia collected 100 tap water samples with the goal of testing whether the chloride level from the samples is significantly higher than the recommended concentration.
A one-sample t-test can be used to test the following hypothesis:
H0: µ≤250
H1: µ>250
To perform a one-sided t-test, the (SIDED=) option can be used:
Example
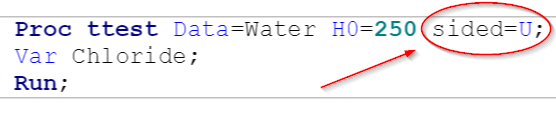
Proc ttest Data=Water H0=250 sided=U;
Var Chloride;
Run;
The (SIDED=U) option tests whether the mean is significantly higher than the hypothesized value (i.e. 250).
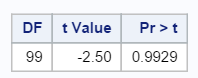
The following t-value and p-value are generated:
The following t-value and p-value are generated:
The p-value is 0.9929, which fails to reject the null hypothesis that the mean chloride concentration is less than 250 mg/L.
The water is safe for consumption indeed!
(SIDED=) Option
There are three values that can be specified for the (SIDED=) option:
- 2: 2-sided test (default)
- U: Upper 1-sided test
- L: Lower 1-sided test
When testing whether the mean is significantly below a specified value, the (SIDED=L) option should be used.
Exercise
Copy and run the BULBS data set from the yellow box below:
Copy and run the BULBS data set from the yellow box below:
The BULBS data set contains a list of 50 testing light bulbs and the number of hours they last before burning out.
A fluorescent light bulb has an average lifespan of 8000 hours.
XYZ-branded light bulb claims to have a significantly longer lifespan than 8000 hours.
Perform a one-sample t-test to check if the claim is valid.
Need some help?
HINT:
The following hypothesis should be tested:
H0: µ≤8000
H1: µ>8000
SOLUTION:
proc ttest data=bulbs h0=8000 sided=U;
var hours;
run;
The p-value is 0.0020, which rejects the hypothesis that the XYZ-branded light bulbs have an average lifespan below 8000 hours.
Fill out my online form.