Sentry Page Protection

Please Wait...

Time Series Modeling
​[10-15]

---

Once you have an approximate stationary time series, the next step is to look at the residuals and see if there is any remaining autocorrelation.

If the residual is pure white noise, you're done! All of the correlation is explained by the model (i.e. differencing and transformation).

If not, you might need to add an AR or MA term to correct the autocorrelation before getting to the final model.

Let's look at the following example.

​Copy and run the code from the yellow box below:

data ts1; input time x; datalines; 1 100.06 2 103.1 3 103.55 4 104.61 5 106.96 6 106.89 7 107.78 8 108.99 9 111.27 10 116.92 11 117.6 12 116.7 13 119.62 14 119.96 15 119.47 16 120.43 17 121.41 18 124.49 19 131.36 20 129.3 21 130.68 22 134.9 23 134.58 24 132.23 25 134.84 26 135.17 27 137.38 28 133.89 29 131.26 30 130.03 31 127.7 32 131.2 33 135.74 34 138.64 35 135.39 36 134.29 37 133.63 38 132.07 39 131.91 40 128.76 41 126.21 42 130.88 43 137.08 44 136.49 45 135.74 46 132.67 47 136.31 48 144.17 49 146.86 50 151.14 51 148.25 52 144.12 53 139.56 54 136.57 55 140.16 56 139.09 57 131.25 58 133.74 59 132.4 60 129 61 123.8 62 121.57 63 124.18 64 122.76 65 115.36 66 114.61 67 113.56 68 115.24 69 117.02 70 118.41 71 113.4 72 119.12 73 120.72 74 120.26 75 124.08 76 124.25 77 119.46 78 116.98 79 116.1 80 119.24 81 113.6 82 108.4 83 108.95 84 113.76 85 117.48 86 112.79 87 115.93 88 115.58 89 117.85 90 114.03 91 113.36 92 108.96 93 109.39 94 115.14 95 112.29 96 114.04 97 111.65 98 112.39 99 110.92 100 115.74 101 116.31 102 114.76 103 111.8 104 114.63 105 112.77 106 109.16 107 106.38 108 105.53 109 103.7 110 106.54 111 105.63 112 102.85 113 109.49 114 109.47 115 105.78 116 107.03 117 104.38 118 100.2 119 98.27 120 98 121 98.55 122 103.19 123 100.61 124 99.49 125 99.43 126 102.74 127 103.73 128 100.54 129 97.45 130 98.8 131 104.87 132 103.7 133 97.62 134 97.13 135 100.17 136 99.25 137 106.74 138 102.55 139 101.9 140 96 141 97.18 142 98.52 143 98.7 144 100.89 145 101.76 146 100.68 147 98.5 148 98.74 149 103.5 150 105.96 151 108.93 152 105.14 153 110.96 154 114.01 155 111.02 156 112.04 157 116.41 158 119.46 159 119.84 160 128.83 161 133.09 162 133.72 163 133.52 164 131.93 165 128.81 166 127.95 167 129.66 168 129.42 169 128.39 170 130.12 171 133.84 172 133.63 173 133.86 174 133.27 175 130.72 176 133.68 177 138.96 178 136.18 179 134.01 180 131.72 181 128.86 182 124.85 183 122.04 184 122.04 185 118.58 186 121.56 187 122.92 188 124.02 189 122.63 190 124.19 191 123.4 192 121.32 193 125.08 194 124.61 195 125.62 196 129.74 197 125.57 198 120.67 199 116.91 200 116.68 ; run;

The TS1 data set contains our usual list of simulated values.

proc arima data=ts1;
identify var=x;
run;
quit;

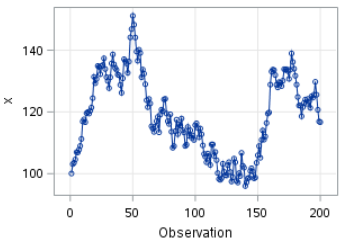
The time series plot shows a non-constant mean:

One order of differencing is needed.

proc arima data=ts1;
identify var=x(1);
run;
quit;​

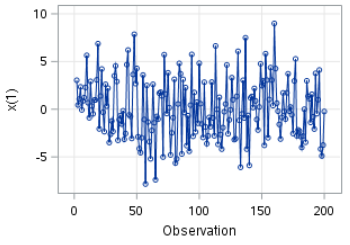
​The time series plot looks great after differencing:

The mean seems to be stabilized with no obvious fluctuation in the variance.

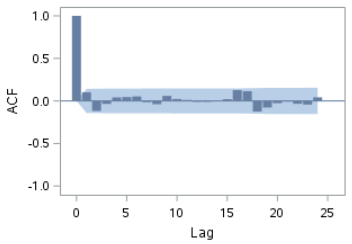
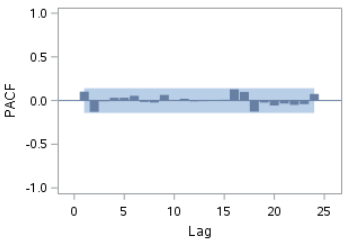
We are now going to look at the ACF and PACF plots:

The ACF and PACF plots show no spike at any lag.

The remaining residual (after differencing) looks like white noise.

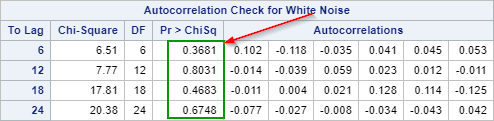
Now, let's look at the Ljung-box test:

The p-values are above 0.05 at lags 6, 12, 18 and 24.

We conclude that the residuals are white noise.

We're done! All of the correlation seems to have been explained by the differencing.

We have tentatively identified the model to be the ARIMA (0 1 0) model.

---

Note:

A non-seasonal ARIMA model is usually written in the form of ARIMA (p, d, q) where:

• p = number of AR terms
• d = differencing order
• q = number of MA terms

In our example, the ARIMA (0 1 0) is the model that has one differencing order and no AR and MA term.

---

Random Walk Model

An ARIMA (0 1 0) model is also called the random-walk model because of its forecasting equation:

Yt - Yt-1 = Wt

where Wt is defined as white noise with a zero mean and constant standard deviation.​

If you move Yt-1 to the other side, you will have:

Yt = Yt-1 + Wt

Yt is just a random walk (white noise) away from Yt-1!
​
In the next few sections, we will look at a number of examples where an AR or MA term is needed to correct the remaining autocorrelation in the residual.

---

Exercise

Copy and run the STOCKS data set from the yellow box below:

data stocks; format date date9.; input date close; datalines; 20820 285.29 20821 309.28 20822 289.4 20823 281.13 20824 288.12 20825 277.36 20826 289.82 20827 282.98 20828 321.71 20829 327.36 20830 349.94 20831 336.49 20832 346.82 20833 360.7 20834 340.42 20835 337.29 20836 323.99 20837 340.09 20838 359.99 20839 351.97 20840 352.85 20841 357.4 20842 359 20843 376.88 20844 403.89 20845 441.23 20846 398.06 20847 411.15 20848 399.27 20849 393.63 20850 398.81 20851 366.25 20852 339.64 20853 322.57 20854 323.75 20855 354.36 20856 362.64 20857 352.8 20858 352.78 20859 343.34 20860 355.51 20861 384.52 20862 406.91 20863 430.25 20864 457.73 20865 498.75 20866 503.31 20867 501.01 20868 543.64 20869 509.03 20870 531.94 20871 556.59 20872 573.24 20873 567.86 20874 579.05 20875 571.88 20876 573.98 20877 614.15 20878 597.59 20879 583.32 20880 612.73 20881 592.18 20882 560.02 20883 561.9 20884 571.26 20885 573.95 20886 569.3 20887 556.5 20888 532.66 20889 528.67 20890 553.85 20891 569.69 20892 598.18 20893 622.46 20894 613.29 20895 618.36 20896 619.31 20897 597.02 20898 590.62 20899 596.81 20900 582.53 20901 584.68 20902 580.33 20903 572.75 20904 589.86 20905 584.06 20906 584.83 20907 585.93 20908 587.23 20909 600.86 20910 638.4 20911 626.91 20912 599.61 20913 613.64 20914 589.59 20915 588.3 20916 606.36 20917 594.57 20918 588.96 20919 555.95 ; run;

​The STOCKS data set contains a list of stock closing prices for 100 days.

Perform one order of differencing to stabilize the mean and check the Ljung-box test results.

Can you conclude that the residuals are purely white noise?

Next

---

Need some help?

Fill out my online form.