Sentry Page Protection

Please Wait...

Time Series Modeling
​[9-15]

---

Seasonal Differencing

Seasonal differencing can be used to stabilize seasonal spikes in a time series.

​Let's look at an example below.

data ex5; input time x; datalines; 1 509 2 505 3 461 4 507 5 492 6 494 7 462 8 484 9 537 10 781 11 465 12 512 13 525 14 476 15 504 16 527 17 529 18 480 19 500 20 901 21 499 22 482 23 553 24 461 25 574 26 485 27 476 28 478 29 514 30 819 31 465 32 529 33 549 34 474 35 481 36 508 37 480 38 458 39 556 40 837 41 546 42 498 43 535 44 537 45 472 46 513 47 473 48 504 49 507 50 763 51 488 52 476 53 435 54 478 55 501 56 512 57 509 58 470 59 485 60 768 61 517 62 489 63 453 64 433 65 489 66 474 67 529 68 474 69 522 70 845 71 484 72 478 73 479 74 492 75 480 76 524 77 470 78 555 79 519 80 854 81 541 82 507 83 484 84 516 85 502 86 561 87 466 88 497 89 488 90 851 91 515 92 441 93 469 94 519 95 490 96 501 97 464 98 499 99 484 100 816 101 477 102 500 103 515 104 477 105 517 106 452 107 478 108 465 109 459 110 703 111 537 112 520 113 496 114 470 115 563 116 474 117 473 118 549 119 487 120 777 121 467 122 546 123 460 124 475 125 498 126 505 127 538 128 508 129 512 130 792 131 542 132 566 133 487 134 537 135 476 136 561 137 460 138 426 139 472 140 757 141 551 142 509 143 472 144 501 145 515 146 530 147 481 148 520 149 492 150 877 151 543 152 515 153 480 154 459 155 539 156 481 157 483 158 490 159 435 160 860 161 481 162 480 163 530 164 510 165 494 166 503 167 522 168 510 169 483 170 880 171 461 172 439 173 524 174 519 175 476 176 465 177 472 178 472 179 502 180 760 181 572 182 508 183 477 184 468 185 532 186 452 187 526 188 491 189 443 190 778 191 567 192 462 193 467 194 548 195 493 196 484 197 494 198 466 199 473 200 781 ; run;

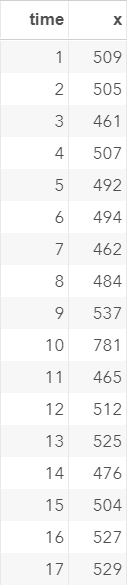
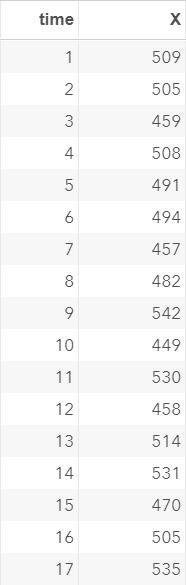
The EX5 data set contains another set of simulated values.

As usual, we'll plot the time series, ACF and PACF:

proc arima data=ex5;
identify var=x;
run;
quit;

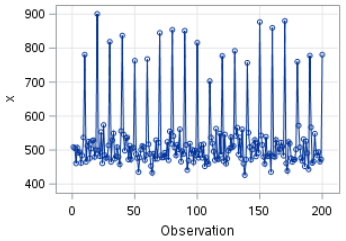
The time series plot shows seasonal spikes every 10 days:

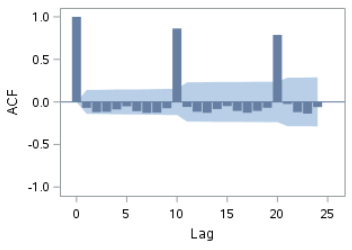
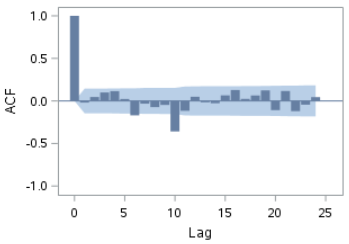
The ACF plot shows seasonal spikes as well:

We are going to try a seasonal differencing with seasonality=10.

​Example

proc arima data=ex5;
identify var=x(10);
run;
quit;

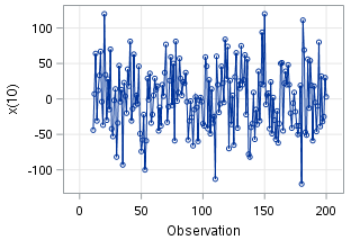
The plot after differencing shows some promising results.

The means are stabilized:

The ACF plot still has spikes at certain lags. However, it is quite an improvement over the ACF plot before differencing.

---

Stabilizing Unequal Variance

When a time series shows increasing or decreasing variance over time, a transformation might be able to fix the issue.

Let's look at an example.

data ex6; call streaminit(100); do time = 1 to 200; p = time/60 + 1; X = round(rand('normal', 500, 30*p), 1); output; end; drop p; run;

The EX6 data set, as usual, contains a list of simulated values:

Let's plot the time series.

proc arima data=ex6;
identify var=x;
run;
quit;

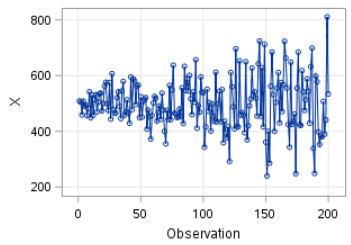
​You can clearly see the time series becoming more volatile as time passes:

​Note: the range of X goes from 200 to 800:

Now, let's plot the time series with log transformation on X:

data ex6a;
set ex6;
y = log(x);
run;

proc arima data=ex6a;
identify var=y;
run;
quit;

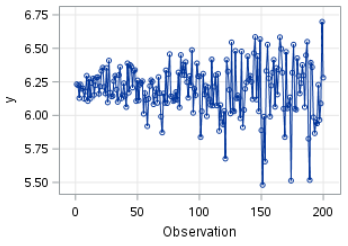
The time series plot for log(y) is shown below:

The variance didn't seem to be stabilized. 

It still shows the same structure as before.

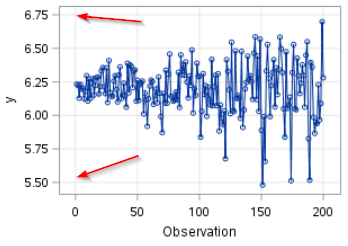
However, if you look at the range of the log(x) value, you will see the range has shrunk to 5.5 to 6.75: 

We are going to plot the time series again, but with a wider range.

This can be done using the SGPLOT procedure:

data ex6a;
set ex6;
y = log(x);
run;

proc sgplot data=ex6a;
series y=y x=time;
yaxis values= (0 to 10) grid;
xaxis grid;
run;

You will see that there is a huge improvement in the variance of the time series.

In the next section, we will learn more about the Autoregressive (AR) model.

---

Exercise

Locate the AIR data set from the SASHelp library.

The AIR data set contains airline passenger data for January, 1949 to December, 1960.

This is a well-known example used for time series analysis.

See Time Series: Forecast and Control by Box, Jenkins and Reinsel (ISBN: 978-0470272848).


Task 1:
Plot the time series, ACF and PACF of the airline passenger data.

Task 2:
Does the time series data look stationary?

If not, use various techniques to transform the series into an approximate stationary series.

Next

---

Need some help?

Fill out my online form.